|
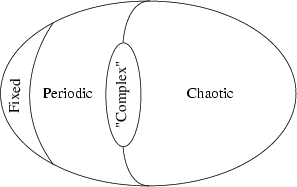
As discussed in the previous section, there are two primary regimes of rules, periodic (Class II) and chaotic (Class III), separated by a third, transition regime (Class IV). Schematically, this appears as Langton's famous egg diagram:

|
The transition regime has proven to be made of a complicated structure. In some
experiments with the ![]() parameter, the transition regime acts as
nothing more than a boundary line between periodic and chaotic behavior. Crossing
over this line (increasing or decreasing
parameter, the transition regime acts as
nothing more than a boundary line between periodic and chaotic behavior. Crossing
over this line (increasing or decreasing ![]() ) produces a discrete
jump between behaviors. Quantitative analysis shows a discrete jump in statistical
measures9 of the kind usually associated with first-order transitions10. In other experiments with the
) produces a discrete
jump between behaviors. Quantitative analysis shows a discrete jump in statistical
measures9 of the kind usually associated with first-order transitions10. In other experiments with the ![]() parameter, the transition regime
acts as a smooth transition between periodic and chaotic activity. This smooth
change in dynamical behavior was described in the experiment discussed in section
parameter, the transition regime
acts as a smooth transition between periodic and chaotic activity. This smooth
change in dynamical behavior was described in the experiment discussed in section
![]() . This type of transition is primarily second-order11, also called a critical transition.
. This type of transition is primarily second-order11, also called a critical transition.
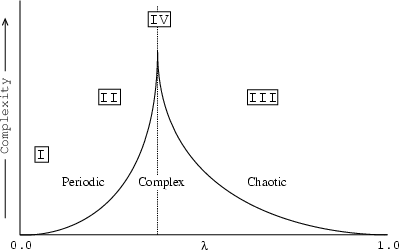
To summarize, giving a qualitative description of CA behavior as the ![]() parameter is varied produces the full spectrum of dynamical behaviors. Furthermore,
the pattern of transient length (a complexity metric) forms a sort of butterfly
pattern; the transition regime acting as the butterfly's body. Thus, we can
order the dynamical behaviors with respect to their
parameter is varied produces the full spectrum of dynamical behaviors. Furthermore,
the pattern of transient length (a complexity metric) forms a sort of butterfly
pattern; the transition regime acting as the butterfly's body. Thus, we can
order the dynamical behaviors with respect to their ![]() -distance
from the critical transition regime. This is precisely what one expects to see
as one approaches and passes through a second-order phase-transition. Typically,
physical systems which pass through this type of phase-transition have transients
that diverge to infinity and behavior becomes maximally complex and unpredictable.
Thus, Langton hypothesized that it is this phase-transition structure which
``is responsible for the existence of most of the surface-level features in
the diverse phenomenology of CA behaviors.''
-distance
from the critical transition regime. This is precisely what one expects to see
as one approaches and passes through a second-order phase-transition. Typically,
physical systems which pass through this type of phase-transition have transients
that diverge to infinity and behavior becomes maximally complex and unpredictable.
Thus, Langton hypothesized that it is this phase-transition structure which
``is responsible for the existence of most of the surface-level features in
the diverse phenomenology of CA behaviors.''
Using this notion of a phase-transition, we describe12 the existence of and relationship between the four Wolfram classes in Figure
![]() .
.
|
A natural question to ask is whether or not this phase-transition structure underlying CA ``phenomenology'' bares any resemblance to the ``phenomenology'' of computations. In other words, we would like to find CA behaviors that parallel the behaviors we see in computation. We already know that CAs can form logical universes in which we may construct universal computers. Hence, we look for analogues of computability and complexity.
The phase-transition structure tells us that near a critical ![]() value, the complexity of CA behavior rapidly increases. What this means is that
it becomes much more difficult to characterize the long-term behavior of CAs
near this critical value. This is primarily due to the increased length of transients.
For relatively13 low values of
value, the complexity of CA behavior rapidly increases. What this means is that
it becomes much more difficult to characterize the long-term behavior of CAs
near this critical value. This is primarily due to the increased length of transients.
For relatively13 low values of ![]() , it becomes quickly clear that the system under
observation is heading towards long-term periodic behavior. For relatively high
values of
, it becomes quickly clear that the system under
observation is heading towards long-term periodic behavior. For relatively high
values of ![]() , it becomes quickly clear that the system under observation
is heading towards long-term chaotic behavior. However, for
, it becomes quickly clear that the system under observation
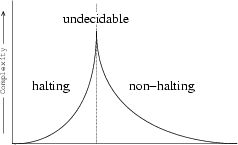
is heading towards long-term chaotic behavior. However, for ![]() near the critical value, either of these long-term outcomes is possible. Coupled
with very long transient lengths, it becomes effectively undecidable as to whether
a given rule set and starting configuration will tend towards periodic or chaotic
behavior. A genesis of the Halting Problem14!
near the critical value, either of these long-term outcomes is possible. Coupled
with very long transient lengths, it becomes effectively undecidable as to whether
a given rule set and starting configuration will tend towards periodic or chaotic
behavior. A genesis of the Halting Problem14!
Complexity classes in computation refer to the time it takes for a halting computation to complete with respect to the size of its input. Typically, these classes have names such as constant, polynomial, and exponential, referring to the class of algebraic formula representing the relation between input size and computation time. The time it takes for a computation to complete can be thought of as the transient time leading to the fixed-point state of solution. Thus, the complexity classes of computation are analagous to the structures produced in answering the question: Given a rule set and starting configuration, how long does it take for the CA to exhibit ``typical'', long-term behavior.
We have been using the notion of an underlying phase-transition structure as
an analogy for discussing the relation between computational and dynamical behaviors.
In fact, what we want to show is that by assuming this underlying phase-transition
structure, we are provided with ``a simple and straightforward explanation
for the existence of, and relationship between, many significant features of
the phenomenology of computation''15. (See Figure ![]() ).
).
|
Langton gave the following four arguments for making this assumption:
Arising out of the existence of a fundamental connection between computation and phase-transitions is a wide variety of beautiful and powerful implications. We briefly discuss the implications introduced at the end of Langton's thesis.
There is a fundamental equivalence between the dynamics of phase-transitions and the dynamics of information processing. This means that computation can be thought of as a special case of phase-transition phenomena and that the theory of computation can be used to explain phenomena in the theory of phase-transitions. Thus, we may look to the natural systems around us for emergent, information processing capabilities.
We all know the three phases of matter: solid, liquid and gas. However, there exists a critical temperature at which the surface between the gas and liquid phases disappears. The resulting matter is known as a supercritical fluid [3]. Thus, we may say that there exists two phases of matter: solid and fluid. What is very interesting is that even though the CA experiments existed in a non-physical substrate, we still ended up with two primary regimes of behavior: the static, solid, dynamics of fixed-point and periodic structures and the non-static, fluid, chaotic dynamics. Langton hypothesizes that the categories, solid and fluid, are not merely material qualities but instead are dynamical qualities separated by a critical transition.
If the phases of matter can indeed be generalized as dynamical qualities, then the difference between a natural and artificial system seems less real. For, if the behavior of matter can be reproduced in a computer world ``then it is only a matter of organization to turn 'hardware' into 'wetware' and, ultimately, for hardware to achieve everything that has been achieved by wetware, and more.''17
If we were to look for a beginning of life, we are tempted to focus on the phase-transitions that were occurring on pre-biotic earth. From them would have emerged information processing abilities. Those abilities may have become coupled with one another to form complex, meta-stable information structures in the physical substrate of earth (the primordial ``soup''). Those structures which gained a local control over their parameters survived, while others were pushed passed the event horizon of an attractor. In this sense, the ``living'' systems are precisely those systems that are able to avoid attractors. Evolution is then a repeated iteration whereby a system climbs out of one attractor into a higher dimensional phase-space, only to find itself heading for a higher dimensional attractor; a Red Queen18.
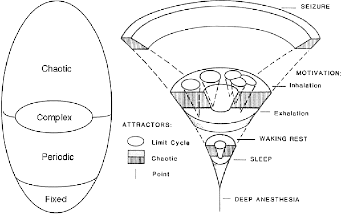
Looking at the processes and structures of living cells, we see the same sort
of phase-transition conditions. A particularly good example of this is the dynamics
of the olfactory bulb which during rest takes on low-amplitude chaotic activity
and during inhalation falls into the basin of a periodic attractor. Thus, the
olfactory bulb spends a good portion of its time in the transition regime between
chaotic and periodic behavior. (See Figure19 ![]() ).
).
|
That a phase-transition structure is underlying CA state space is not just a
convenient analogy for describing how behavior varies with the ![]() parameter. By assuming this structure we are provided with powerful means for
explaining the existence of many of the fundamental features of computational
theory by allowing them to naturally arise out of a dynamical systems context.
Conversely, the dynamical behaviors that are found in dynamical systems near
a critical transition can be explained in terms of the computational abilities
they may harbor. Thus, we are presented with new ways in which we may analyze
and reanalyze both the natural and artificial systems surrounding us.
parameter. By assuming this structure we are provided with powerful means for
explaining the existence of many of the fundamental features of computational
theory by allowing them to naturally arise out of a dynamical systems context.
Conversely, the dynamical behaviors that are found in dynamical systems near
a critical transition can be explained in terms of the computational abilities
they may harbor. Thus, we are presented with new ways in which we may analyze
and reanalyze both the natural and artificial systems surrounding us.
Average mutual information was plotted against the single cell entropy. This
plot gave away that the transition regime optimized system entropy to handle
both storage of information (which reduces entropy) and transmission of information
(which increases entropy). The plot took on the same shape that is characteristic
of thermodynamic phase-transition graphs; particular, the ![]() -transition
[3].
-transition
[3].