Quaternion interpolation

For various reasons, interpolation rotation with Euler angles is less than ideal. A naive approach to rotational interpolation could be to simply interpoloate between each Euler angle to produce inbetween frames. But the motion specified by such a rotation is oftentimes jerky and ill specified. This is illustrated by there not being a unique path between every two orientations across different coordinate systems. For these reasons quaternion interpolation of the rotational parameters is performed. Interpolating in quaternion space ensures a unique path under all circumstances.

Since Euler angles present a more agreeable user interface, the process of quaternion interpolation starts by generating a rotation matrix R from a set of Euler angles. This matrix is then lifted into quaternion space where the rotation is specified by a quaternion where v specifies an axis of rotation and the angle by which to rotate around the axis. Note that q is a unit quaternion, so the set of rotation matrices corresponds to the set of quaternions on the unit hypersphere.

Rotation can then be carried out directly in quaternion space by encoding a point to be rotated as a pure quaternion and producing a rotated pure quaternion q_r by q_r=qq_pq^-1. It is oftentimes beneficial to concatenate other transformations along with rotations however, so after interpolation q is transformed back into a rotation matrix.

Since the set of quaternions that specify rotations live on the unit hypersphere, a direct interpolation between quaternions does not produce the desired result, as interpolants would stray from the hypersphere. Instead a spherical interpolation is performed. This procedure is outlined in [watt92].

spherical interpolation

The function slerp does a spherical linear interpolation between two quaternions A and B by an amount :

$$\textrm{slerp}\left( A,B,u\right) =A\frac{\sin \left( 1-u\right) \Omega }{\sin \Omega }+B\frac{\sin \Omega u}{\sinh \Omega }.$$

To achieve C² continuity between curve segments, a cubic interpolation must be done. In quaternion space this is somewhat complicated. The method used is to compose a cubic interpolation as a set of three linear interpolations. First between the data points and two other (carefully chosen) points, and then between the remaining points by an amount specified by the logistic equation with r=2. If the auxiliary points are chosen properly, then C² continuity can be ensured. The function squad does a cubic interpolation between data points b₀ and b₃ by an amount

$$\begin{array}{l} \textrm{squad}\left( b_{0},S_{1},S_{2},b_{3... ...S_{1},S_{2},u\right) ,2u\left( 1-u\right) \right) \end{array}.$$

The points S₁ and S₂ are called inner quadrangle points, and have to be chosen carefully so that continuity is guaranteed across segments. Given a quadrangle of quaternions, where q_i and q_i+1 are our data points, we can guarantee C² continuity by choosing a_i and a_i+1 as follows:

$$a_{i}=q_{i}e^{\left( -\frac{\textrm{ln}\left( q_{i}^{-1}q_{i... ...ight) +\textrm{ln}\left( q_{i}^{-1}q_{i-1}\right) }{4}\right) }$$

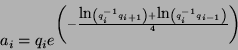
For more information see [shoe87].

We can summarize the process of interpolating between two rotation matrices as follows

  

interpolate_rotation(mat[n],t)

  t_int = int(t);

  t_fract = t - t_int;

  

  q_0 = mat2quat(mat[t_int-1]);

  q_1 = mat2quat(mat[t_int]);

  q_2 = mat2quat(mat[t_int+1]);

  q_3 = mat2quat(mat[t_int+2]);

  

  i_1 = inner_quad_point(q_0, q_1, q_2);

  i_2 = inner_quad_point(q_1, q_2, q_3);

  

  q_i = slerp(slerp(q_1, q_2, t_fract),

              slerp(i_1, i_2, t_fract),

              2*t_fract*(1-t_fract);

  

  return mat2quat(q_i);