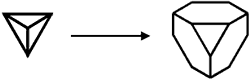
Truncations are the main method of changing a regular polyhedron into a new semi-regular (1) polyhedron. The word "truncate" is specifically the act of symmetrically slicing away pieces. There are two different types of truncations that can be performed to create the new semi-regular polyhedrons. The first type, from now referred to as plain old "truncating", is done by making slices at a vertex. "Truncating a regular tetrahedron, by symmetrically slicing off each vertex, produces a new equilateral triangle at each vertex and changes each face into a hexagon."(2)

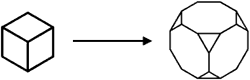
The truncated square is formed in much the same way: Remove the corners to make equilateral triangles, and the original square faces of the cube become octagons. Since four faces meet at the vertexes of the octahedron, cutting off itís corners makes squares, and the original triangular faces become hexagons.
 |
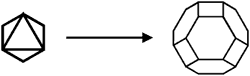 |
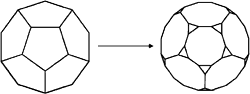
The dodecahedron and the icosahedron can be truncated in a similar way.
 |
 |
The second type of truncation, from now referred to as "double-truncating", is done by making slices along the edges and along the corners. A good example of double-truncating is the easy to see double-truncated cube. The slice along each edge creates a square at each edge, and a slice along each corner makes a triangle at each corner.
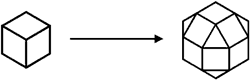
The octahedron can also undergo these modifications. The double-truncated octahedron is shown below.
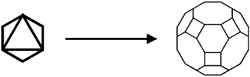
One might come to the question: "Can you truncated a truncated polyhedron further?" The answer of course is yes! Letís take a look at continuing the truncation of the truncated cube first. For instance, rather than truncating the corners of a cube to give equilateral octagons in place of the original squares on the cube, the cuts can extend until they meet at the midpoint of each edge. This gives a square, tilted at 45į in the place of each original square. Now letís truncate the truncated octahedron. Again, the cuts extend to the center of the edges, making the original triangular faces back into triangles.
Truncating both the cube and the octahedron in this way forms the same shape, consisting of 8 triangles and six squares. This is known as the cuboctahedron and can be considered the essence of the cube/octahedron duality.

What would happen if we continued to truncate the truncated tetrahedron? Continuing the truncation of the tetrahedron, the original triangular faces become triangles, and each vertex becomes a triangle. This yields an octahedron, strangely, rather than some truncation of the tetrahedron.

There are several ways to interpret this strange fact. One way is to realize that an octahedron with alternating tetrahedrons on four of its faces is a larger tetrahedron. Another way is to notice that when a polyhedron is truncated, the number of new faces is equal to the number of original faces plus the number of original corners. For the tetrahedron, this is 4+4, yielding a new 8 sided object, with regular triangular faces. The octahedron fits the bill.
While we are performing this truncating trickery, letís continue the truncation of the double-truncated polyhedra constructed earlier. Do you have any guesses as to what will come out? Letís first truncate the double-truncated cube. The cutting planes move inward, until they finally meet at the centers of the faces of the original cube. The shape that results is the octahedron. This happens because the dual of the cube is the octahedron, and truncating along planes that meet in the centers of the faces is the same as constructing the dual of the original shape.
The octahedron! And for the same reason, truncating the double-truncated octahedron gives use the cube.
What about the tetrahedron? We have yet to create its double-truncated analog. Take a moment and try to guess what will result. Surprisingly, truncating along the edges and corners of the tetrahedron yields four new triangular faces on the vertexes and six square faces along the edges. Add these to the original four faces, now shrunken, and you have a cuboctahedron. And, to top it all off, continuing this truncation to the centers of the tetrahedronís faces yields a tetrahedron, since tetrahedrons are self-dual.
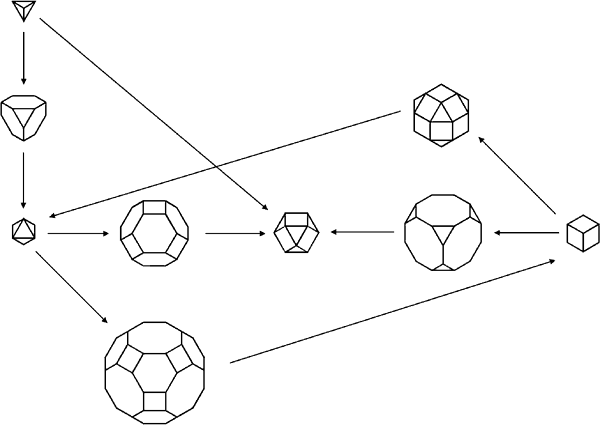
This complex set of relations and similarities could be thought of as the tetrahedron-cube-octahedron family of regular and semi-regular polyhedra. The dodecahedron and the icosahedron, also duals, have their own family of regular and semi-regular polyhedra. Unfortunately, there is no sixth, self-dual, regular polyhedron that can be stuck inside one or the other of these, and so the relationship is less intricate than that of the tetrahedron-cube-octahedron family. In fact, this may be the reason that these shapes may not tile space at all.
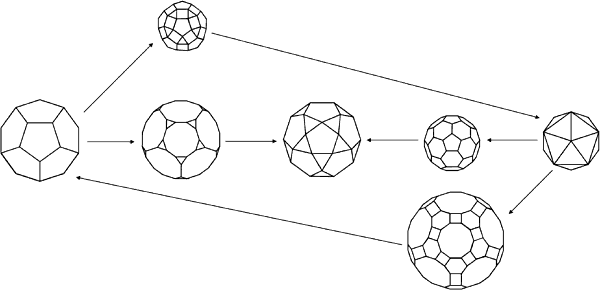
All the truncated shapes of a group consist of the combined symmetries of the simple polyhedra in the group.
1. Semi-regular polyhedrons are regular in the sense that the polygons making up their faces are regular polygons. There can be multiple different polygon faces in one polyhedron and because of this equal angles between faces is lost. Each vertex must still be identical, i.e. all must have the same number of polygons around the vertex.
2. The Penguin Dictionary of Curious and Interesting Geometry, p. 180