Inversion

Inverting $\Bbb{S}^{n-1}$ inside $\Bbb{S}^{n}$

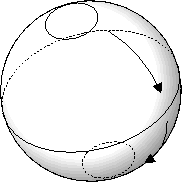
From our two balls model, it is easy to see that we can shrink the equatorial $\Bbb{S}^{n-1}$ inside $\Bbb{S}^{n}$, until it is a small sphere surrounding the north pole or the south pole.

Let $\ensuremath{\vec{\mathrm{\mathbf{x}}}} \in \ensuremath{\Bbb{S}^{n-1}}$, and let $P(\ensuremath{\vec{\mathrm{\mathbf{x}}}}): \ensuremath{\Bbb{S}^{n+1}} \rightarrow \ensuremath{\Bbb{R}^{n-1}}$ such that $\ensuremath{\vec{\mathrm{\mathbf{x}}}}\mapsto \left( \ensuremath{\vec{\mathrm{\mathbf{x}}}}\sin\theta, \cos\theta\right)$. Then varying $\theta$ in the range $-1 \leq \theta \leq 1$ gives a continuous family of $\Bbb{S}^{n-1}$ inside $\Bbb{S}^{n}$. When $\theta = 1$ or $-1$, the sphere is shrunk to a single point. When $\theta$ is close to 1 or -1, it's a little sphere around either the north or south pole. When $\theta$ is near zero, it is nearly equatorial.

If we now consider the two regions into which the $\Bbb{S}^{n}$ is divided by this moving $\Bbb{S}^{n-1}$, this might seem very similar to some process of turning the $\Bbb{S}^{n-1}$ ``inside out.'' However, this is not quite correct. We might look at the $\Bbb{S}^{n-1}$ inside $\Bbb{S}^{n}$ at some point and label the two regions as ``inside'' and ``outside'' based on which region was smaller. We do this because we are used to Euclidean space, where the ``inside,'' of a closed region usually appears smaller, and the outside usually includes the point at infinity.

However, the region inside the sphere is already finite, and so calling this process ``inverting,'' or swapping the ``inside'' and ``outside'' of $\Bbb{S}^{n-1}$ inside $\Bbb{S}^{n}$ really doesn't make a whole lot of sense. All we can say is that we can distort $\Bbb{S}^{n-1}$ inside $\Bbb{S}^{n}$ in such a way as to shrink one region down to a point while expanding another region from a point to the whole sphere.

Following from this, we see that any closed surface inside $\Bbb{S}^{n}$ can be ``inverted,'' by simply gluing $\Bbb{S}^{n-1}$ to a small region of the manifold, and then ``inverting'' this sphere.

From now on I'll use the word ``inversion'' in the sphere to mean a process like this which apparently reverses the two regions in $\Bbb{S}^{n}$ created by a dividing surface in $\Bbb{S}^{n}$.

Inverting $\mathrm{\mathbf{T}}^{n-1}$ inside $\Bbb{S}^{n}$

Notice that $\mathrm{\mathbf{T}}^{1}$ and $\Bbb{S}^{1}$ are identical manifolds. So we know, trivially, that we can invert $\mathrm{\mathbf{T}}^{1}$ inside $\Bbb{S}^{2}$.

Notice also that we can embed the flat torus, $\mathrm{\mathbf{T}}^{2}$, inside $\Bbb{S}^{3}$. To see this best, consider our space to be $\mathbb{C}^2 = \ensuremath{\Bbb{R}^{4}}$. Then the sphere consists of all points $(z_1, z_2)$ such that $\sqrt{ \vert z_1\vert + \vert z_2\vert} = 1$, and the torus consists of all points $(z_1, z_2)$ such that $\vert z_1\vert = \vert z_2\vert = \frac{1}{\sqrt{2}}$.

Inside $\Bbb{S}^{3}$, this torus can be ``inverted,'' that is, it can be deformed in such a way so that (1) the generators of the torus are swapped, and (2) the apparent ``outside'' is swapped with the apparent ``inside.'' Here are a series of pictures to illustrate the second point; pictures showing the generators being swapped are in section 4.2.

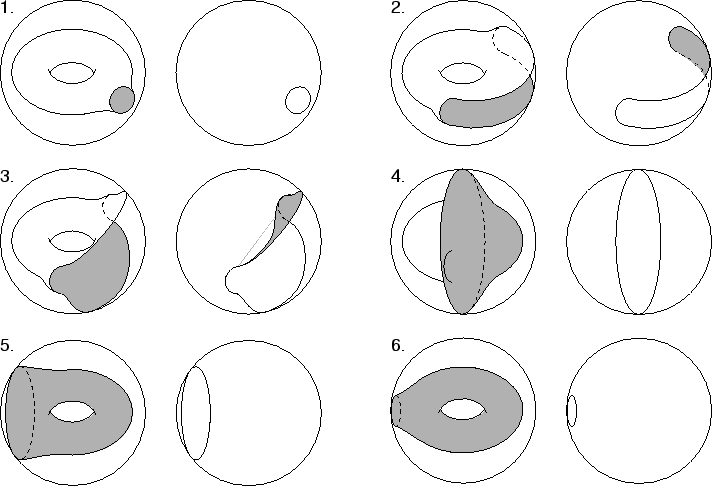
The important point to notice from this is that $\mathrm{\mathbf{T}}^{2}$ divides $\Bbb{S}^{3}$ into two regions, both of which are topologically equivalent to a filled $\mathrm{\mathbf{T}}^{2}$. It is by no means obvious that this is a general fact about $\mathrm{\mathbf{T}}^{n-1}$ inside $\Bbb{S}^{n}$. Furthermore, we can ask whether there is any deeper structure behind this inversion, or whether it is merely a manifestation of the fact, noted above, that any manifold can be inverted inside of the sphere.

Inverting $\mathrm{\mathbf{T}}^{n-1}$ inside $\Bbb{S}^{n}$

We know that any manifold can be inverted inside $\Bbb{S}^{n}$ by gluing it to a sphere. If we know that $\mathrm{\mathbf{T}}^{n-1}$ in general can be embedded inside $\Bbb{S}^{n}$, then we will know that $\mathrm{\mathbf{T}}^{n-1}$ can be inverted inside $\Bbb{S}^{n}$, by gluing the torus to a $\Bbb{S}^{n-1}$ and inverting that $\Bbb{S}^{n-1}$.

The proof is inductive. To begin with, we know that $\mathrm{\mathbf{T}}^{2}$ can be embedded in $\Bbb{R}^{3}$, which can be stereographically projected to $\Bbb{S}^{3}$.

If, in general, $\mathrm{\mathbf{T}}^{n-1}$ can be embedded in $\Bbb{R}^{n}$, then we can embed $\ensuremath{\mathrm{\mathbf{T}}^{n-1}}\times I$ in $\Bbb{R}^{n}$. Think of this simply as as a ``thickened'' or ``fattened'' torus. Next, we cross both with $I$, to get $\ensuremath{\mathrm{\mathbf{T}}^{n-1}}\times I\times I \subset \ensuremath{\Bbb{R}^{n}}\times I$. Now, we can draw a little circle in $I\times I$ to see that $\ensuremath{\mathrm{\mathbf{T}}^{n}} \subset \ensuremath{\mathrm{\mathbf{T}}^{n-1}}\times I\times I$. And, of course, $\ensuremath{\Bbb{R}^{n}}\times I \subset \ensuremath{\Bbb{R}^{n+1}}$. So $\ensuremath{\mathrm{\mathbf{T}}^{n-1}} \subset \ensuremath{\Bbb{R}^{n}} \implies \ensuremath{\mathrm{\mathbf{T}}^{n}} \subset \ensuremath{\Bbb{R}^{n+1}}$. Since $\mathrm{\mathbf{T}}^{n}$ can be embedded in $\Bbb{R}^{n+1}$, $\mathrm{\mathbf{T}}^{n}$ can be embedded in $\Bbb{S}^{n+1}$ as we can just project $\Bbb{R}^{n+1}$ to $\Bbb{S}^{n+1}$ via stereographic projection.

So, in general, $\mathrm{\mathbf{T}}^{n}$ can be embedded and ``inverted'' inside $\Bbb{S}^{n}$. The next question is whether the neat symmetry of $\mathrm{\mathbf{T}}^{2}$ in $\Bbb{S}^{3}$ generalizes as well. To do this we will need to look closer at the structure of $\Bbb{S}^{3}$.