Overview of the Sphere

Definitions

Definition of the Sphere

The n-dimensional sphere is the set of all points in $n+1$ space at a given radius from a center point. The radius is denoted by $r$ and the center by $\vec{\mathrm{\mathbf{c}}}$.

$\ensuremath{\Bbb{S}^{n}} = \left\{ \ensuremath{\vec{\mathrm{\mathbf{x}}}}\ \in... ...ert\ \sqrt{\overset{n+1}{\underset{i=1}{\sum}}{ (x_i - c_i)^2 } } = r \right\}$

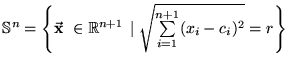
Unless otherwise stated, the center of the sphere is assumed to be $\vec{\mathrm{\mathbf{0}}}$ and the radius is assumed to be 1. Under this definition, $\ensuremath{\Bbb{S}^{0}}$ is the two points $\left\{ 1, -1 \right\}$ in $\Bbb{R}^{1}$, $\Bbb{S}^{1}$ is the unit circle in $\Bbb{R}^{2}$, and $\Bbb{S}^{2}$ is the object which is commonly called the sphere or globe, in $\Bbb{S}^{3}$.

Definition of the N-Disk or N-Ball

An n-Disk is simply the set of all points inside $\Bbb{S}^{n-1}$, or all points less than or equal to $r$ units away from the center $\vec{\mathrm{\mathbf{c}}}$.

$\mathbf{\mathrm{D}}^{n} = \left\{ \ensuremath{\vec{\mathrm{\mathbf{x}}}}\ \in\... ...ert\ \sqrt{\overset{n}{\underset{i=1}{\sum}}{ (x_i - c_i)^2 } } \le r \right\}$

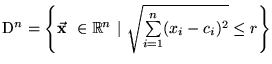
Under this definition, the 1-disk is the line segment between $r$ and $-r$ on $\Bbb{R}^{1}$, the 2-disk is the interior of the circle of radius $r$ in $\Bbb{R}^{2}$, and the 3-disk or 3-ball is the interior of the sphere of radius $r$ in $\Bbb{R}^{3}$. As above, the center is assumed to be $\vec{\mathrm{\mathbf{0}}}$ and the radius to be 1 unless otherwise specified.

Definition of a Manifold

Throughout this paper I will use the term manifold in its standard topological sense. A n-dimensional manifold is usually defined as a set with a collection of patches, or 1-1 functions from $D \rightarrow M$, where $D$ is an open subset of $\ensuremath{\Bbb{R}^{n}}$, such that the following two conditions are satisfied:

(i.) The images of the patches cover $M$

(ii.) For two patches $\tau$ and $\sigma$, the composition $\tau^{-1}\sigma$ and $\sigma^{-1}\tau$ are differentiable and defined on open sets in $\Bbb{R}^{n}$ (O'Neill).

Definition of $\times$, or Cartesian product

The $\times$ operator is the Cartesian product. It takes two manifolds of dimension $n$ and $m$, and duplicates the one at every point along the other, creating a manifold of dimension $m+n$.

Definition of Generator

A generator is a manifold $M$ contained in another manifold $P$ such that $M$ crossed with some other manifold $N$ makes $P$. In other words, if $M \times N = P$, then $M$ and $N$ are generators of $P$. For example, since $\ensuremath{\mathrm{\mathbf{T}}^{2}} = \ensuremath{\mathrm{\mathbf{T}}^{1}} \times \ensuremath{\mathrm{\mathbf{T}}^{1}}$, the generators of $\mathrm{\mathbf{T}}^{2}$ are the two $\mathrm{\mathbf{T}}^{1}$.

Definition of Equator

An equator inside $\Bbb{S}^{n}$ is a $\Bbb{S}^{n-1}$. This can be seen by setting one of the coordinates, say $x_{n+1}$, to zero, and taking all remaining points in $\Bbb{S}^{n}$.

$\left\{ \ensuremath{\vec{\mathrm{\mathbf{x}}}}\ \in\ \ensuremath{\Bbb{R}^{n+1}... ...t{n}{\underset{i=1}{\sum}}{x_i}^2 } = r \right\} = \ensuremath{\Bbb{S}^{n-1}}$

Construction of $\Bbb{S}^{n}$ by two N-disks

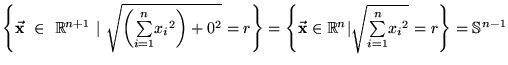
It's fairly trivial to see that two line segments, each end of one segment joined to an end of the other segment, make a circle (or something that can be deformed into a circle). However, the process generalizes to all dimensions, and provides us with a technique of visualizing $\Bbb{S}^{n}$.

Two 2-disks, or filled circles, can be joined along their circular boundaries, to make $\Bbb{S}^{2}$. Each disk makes a hemisphere, and the boundary between the two becomes the equator.

In general, an equator as defined above is $\Bbb{S}^{n-1}$ in $\Bbb{S}^{n}$. Now, all the other points in $\Bbb{S}^{n}$ are the points where $x_n \ne 0$. So the other points in $\Bbb{S}^{n}$ are split into two groups: $x_n > 0$ and $x_n < 0$. We can see that these two sets of points are N-disks because we can let $x_n$ range from 1 to 0, and get a corresponding $\Bbb{S}^{n-1}$ for each value of $x_n$.