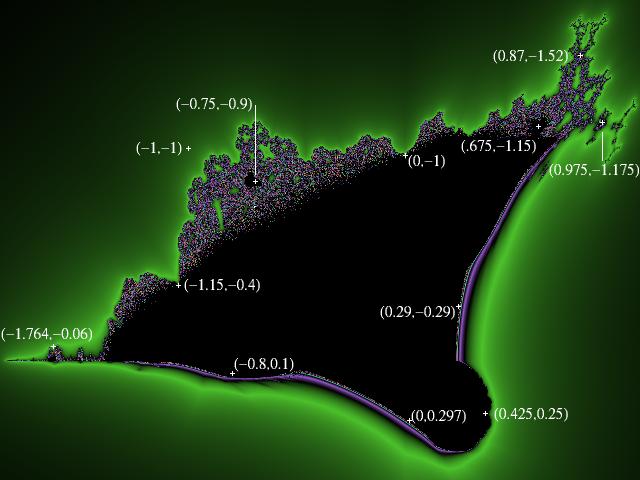
Julia Sets from the Burning Ship
The Julias taken from along the real axis are identical to Julias taken from the z -> z2 Mandelbrot. This happens because if y=0, z2 = x2 = |x|2.
The Burning Ship and the Mandelbrot do not share Julias for any other poins where y!=0. This is because the orbits of all points will eventually take a point to somewhere in the second or fourth quadrants (-x,y) or (x,-y). The y value of the next iteration from within one of these quadrants will be i*2*|-x|*|y| or i*2*|x|*|-y|. Neither of these are the same as the y-value for a point iterated through the Mandelbrot, i*2*x*y, because of the absolute value operation .
To show that all points will pass through this condition, all we need to show is that the coordinates will eventually have opposite sign. If a point is already in one of these quadrants, our condition is satisfied. If not, we have three conditions.
First, if x2 = y2, then our series goes as follows:
(x, y)
(x2-y2, 2*|x|*|y|) = (0, 2*|x|*|y|)
(0-(2*|x|*|y|)2, 2*0*2*|x|*|y|) = (-(2*|x|*|y|)2, 0) = (-x, 0)
Second, if x2 < y2,then our series goes as follows:
(x, y)
(x2-y2, 2*|x|*|y|) = (-x, y)
Third, if x2 > y2,then our series goes as follows:
(x, y)
(x2-y2, 2*|x|*|y|) = (x, y)
((x2-y2)2-4*x2*y2, 2*2*|x|*|y|*(x2-y2) )
Which simplifies to:
(x4-6*x2*y2+y4, 4*|x|3*|y|-4*|y|3*|x|)
By looking deeper in to the iterations, you can continually eliminate smaller and smaller chunks of the fractal. I believe that there is probably some inductive way to show that the rest of the julias are different than the Mandelbrot set's.
Burning Ship Home