next up prev
Next: Ray Casting algorithm Up: Ray Caster Previous: Ray Caster


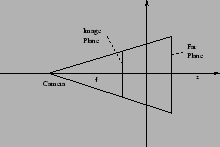
Camera Model

The Camera model is defined as follows:

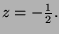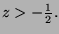
The camera is by default looking down positive z, at the image plane at \( z=-\frac{1}{2}. \) The distance from the image plane to the camera is the focal length f. The far plane can be placed at any \( z>-\frac{1}{2}. \)

To Transform points from quaternion coordinates to camera coordinates, the following transformation is applied: \( p_{c}=R_{c}\left( R_{q}S_{q}p_{q}+T_{q}+T_{c}\right) -T_{c}. \)

pc
The point in camera coordinates.
Rc
The camera rotation matrix. This matrix rotates the camera. It is applied after the camera has been translated to the origin so that rotation is about the projection point.
Rq
The quaternion fractal rotation matrix. It is applied when the julia set is centered at the origin.
Sq
The fractal scaling matrix. It is also applied when the julia set is centered at the origin.
pq
Quaternion point. The point \( p_{q}=\left[ \begin{array}{ccc} x_{q} & y_{q} & z_{q} \end{array}\right] \) defines a quaternion \( q=\left[ \begin{array}{cccc} x_{q} & y_{q} & z_{q} & 0 \end{array}\right] . \)
Tq
The quaternion translation vector. This is applied after rotating and scaling pq.
Tc
Camera translation vector. \( T_{c}=\left[ \begin{array}{ccc} 0 & 0 & f+\frac{1}{2} \end{array}\right] . \) This is used to rotate the camera by translating the projection center to the origin.

Camera Model

\resizebox*{0.4\textwidth}{!}{\includegraphics{camera.eps}}

next up prev
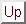
Next: Ray Casting algorithm Up: Ray Caster Previous: Ray Caster
brian martin
1999-06-23