A visualization of The Clifford Tori, Triangulation, and Surgery

Consider this picture of $\Bbb{S}^{3}$ where both the triangulation into sixteen tetrahedral regions (section 5.2) and the equatorial torus (section 4.1) are visible.

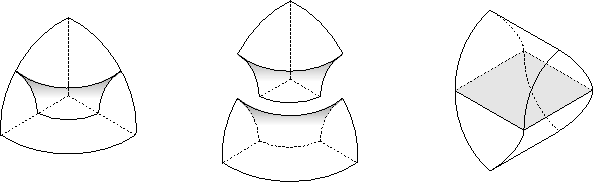
Let us consider now just a single tetrahedral cell. By symmetry, we know that each tetrahedral cell is identical. $\frac{1}{16}$th of the equatorial torus is visible inside this tetrahedron. With a little examination, we can see that this section of the equatorial torus is a square, and we can also tell that it divides the tetrahedron into two similarly shaped triangular prisms. Now we can distort out tetrahedral cell until the section of the equatorial torus is a flat square and the two triangular prisms are the same shape.

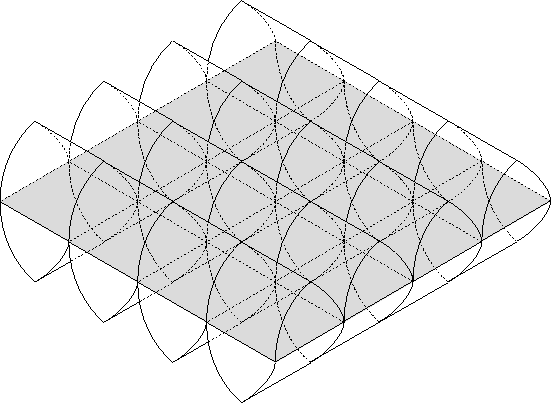
Now, arrange all sixteen tetrahedral regions of $\Bbb{S}^{3}$, so that they are just touching along the edges of the sections of the equatorial torus which divide them. Arranged in this way, we have another picture or ``map'' of $\Bbb{S}^{3}$. If we were to pull the four ridges along the top of this object together into a single line, and pull the four ridges along the bottom together into a single line, we would form the two centerlines of the Clifford Tori. Then if we glued the edges of the equatorial torus, we would wrap this object up into $\Bbb{S}^{3}$.

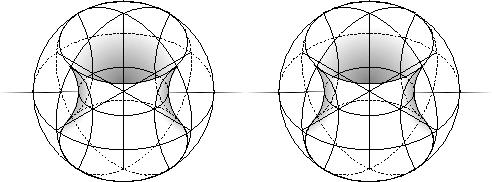
If we separate these sixteen tetrahedra into two $2\times 4$ groups of eight tetrahedra each, we can collapse each section into one of two spheres, each with half of the equatorial torus inside, similarly to what we see in section 4.1. If we separate the sixteen tetrahedra along the surface of the equatorial torus, we can wrap each half up into a filled torus, showing that $\Bbb{S}^{3}$ can be thought of as two filled tori, as in section 6.1.1.

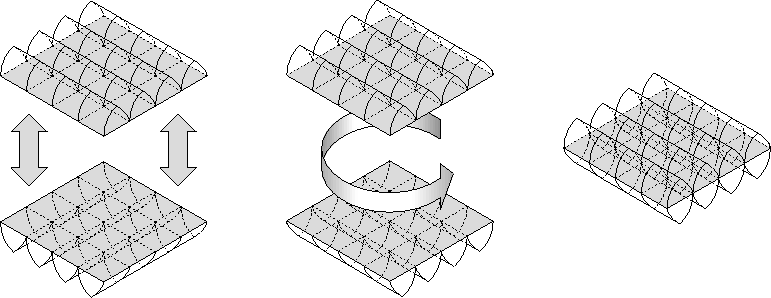
If we separate the sixteen tetrahedra along the surface of the Clifford Tori, rotate one by $\frac{\pi}{2}$, and then reglue the tetrahedra, we have actually performed the surgery on the unknot mentioned in section 6.

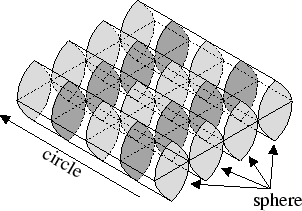
This new manifold appears to be made up of many spheres (here colored alternating shades of gray), arranged in a circle. In other words, it is $\ensuremath{\Bbb{S}^{2}} \times \ensuremath{\Bbb{S}^{1}}$. Here is a picture with five different spheres colored in (Actually, the last one and the first one are the same sphere).