 |
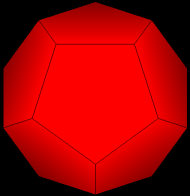
| 1. Start with a single dodecahedron. |
 |
| 2. Now add one dodecahedron on each face of the first dodecahedron. First add one in the back, and five around that. |
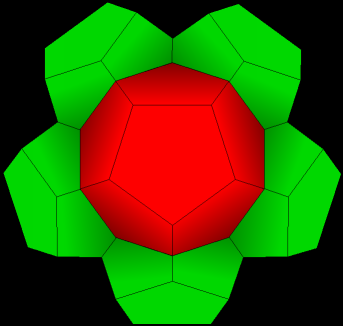 |
| 3. Now we have seven. (one is directly in back and not visible) |
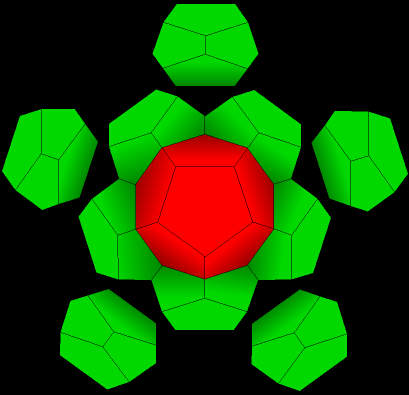 |
| 4. Add five more, and finally a twelfth right in front. |
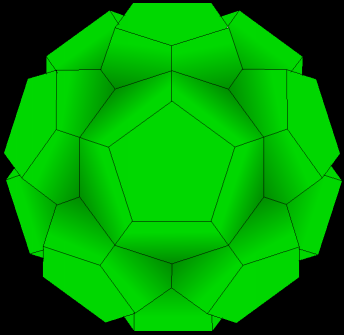 |
| 5. Now we have one central dodecahedron with twelve around it, for a total of thirteen dodecahedra. Notice that there are now twenty little indentations or dimples, one corresponding to each vertex of the original red dodecahedron. Only five are really visible, but if you compare their location to the original dodecahedron, you can see that they are in the same location. |
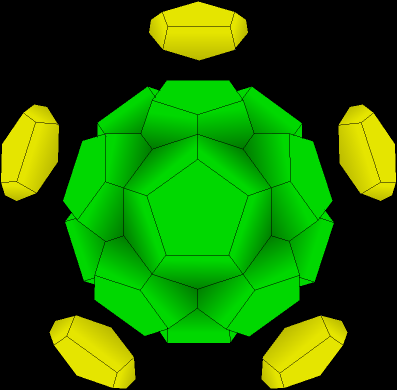 |
| 6. We now add one dodecahedron in each of the twenty dimples. In this step we add ten (five of which are in the rear and not visible) |
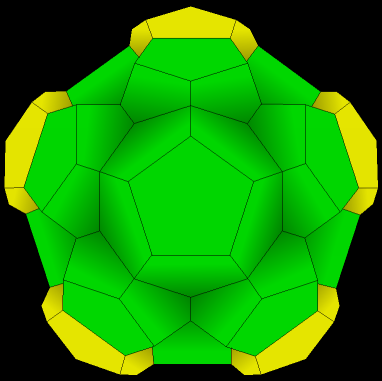 |
| 7. Now we have twenty three. |
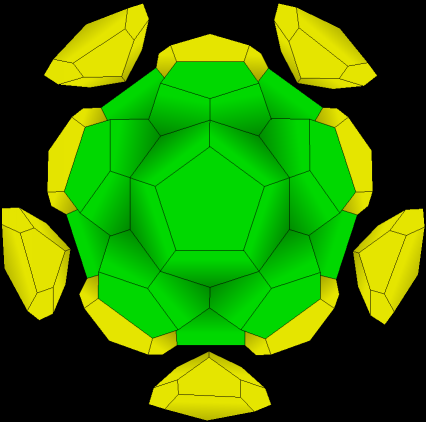 |
| 8. Now add five more. |
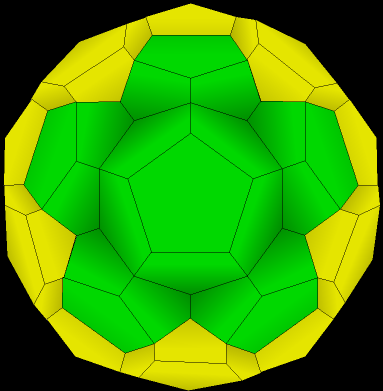 |
| 9. Now we have twenty eight. |
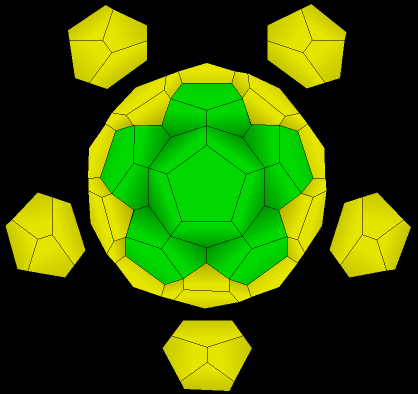 |
| 10. Finally, add the last five. |
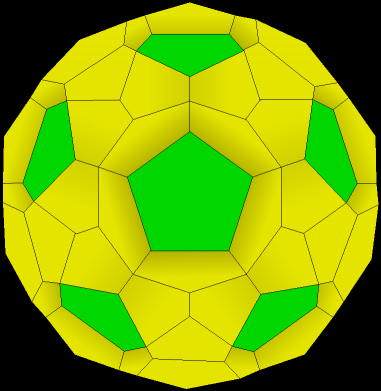 |
| 11. Now there are thirty-three (1 + 12 +20) dodecahedrons. Notice that there are now twelve dimples, corresponding to each of the faces of the original dodecahedron. (look at the green faces). |
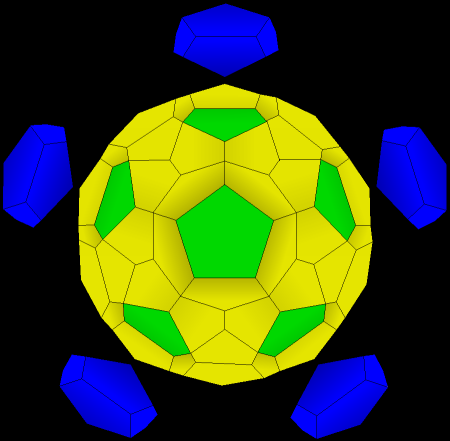 |
| 12. Now we add dodecahedra in each of these spaces. First add one directly in back, then five around it (all not visible here), then five more, that you see here, and finally a last one right in front. |
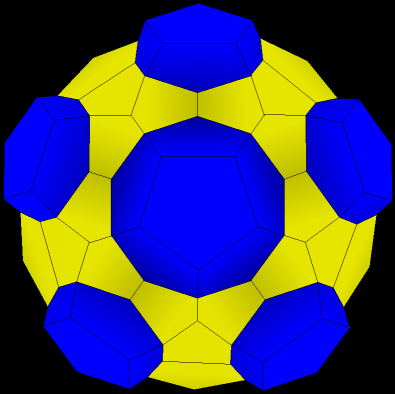 |
| 13. Now we have 45 ( 1 + 12 + 20 + 12 ) dodecahedra. Again, we look for dimples. They are hard to see because the shapes are beginning to get stretched and flattened. They are where two of the yellow dodecahedra come together. Again, they also correspond to parts of the original dodecahedra- this time, the edges. Ten of them are visible, but only five here look like dimples. |
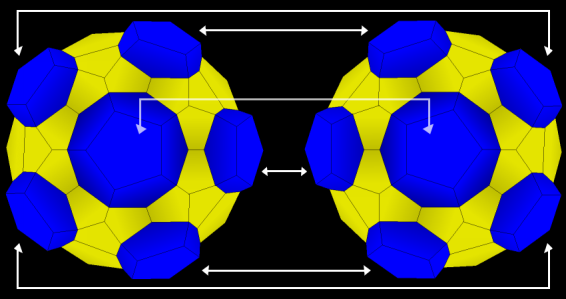 |
| 14. This shape we have built is the "hemi-hypersphere." We take another one just like it and join the blue faces together. The yellow faces leave some empty spaces. These spaces turn out to be just right for thirty more dodecahedra. Each of these last thirty dodecahedra shares four faces with the shape on the left, four faces with the shape on the right, and four with others of the same set. |
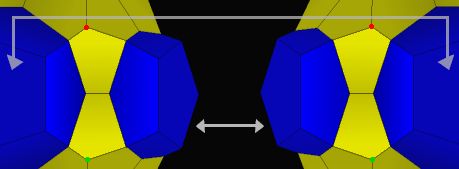 |
| 15. Here's a closeup of how a space for one of the last thirty dodecahedra is formed. The light areas are the eight existing faces. Remember that the blue faces with the arrows are the same faces. All that is left is to connect the remaining four vertices (the red dots to each other, and the green dots to each other) with an edge. We are left with a dodecahedron. The grand total of shapes is 45 + 45 + 30 = 120. Recalling that in this shape we have four cells per vertex and three per edge, a little calculation yields the following table: . vertices edges faces cells 600 1200 720 120And these values satisfy Euler's Formula for elliptic geometry: V + F = E + C. |