Model Definition

In our conversations about how to design our Hydractinia, we focused on several key questions:

1. Agent-based or cellular automata based simulation?
2. How realistic (both in terms of implementation and model realism) is basing fight-resolution on the global property of colony size?
3. Were we to calculate colony size, how would we determine the size of a colony after it fuses with another?
4. What neighborhood (von Neumann or Moore) should be used for a) counting nearby mat cells b) reproducing and c) fighting?
5. With passive rejection (between two fused mat colonies), should failing to allorecognize the other colony inhibit reproduction, as it does with aggressive rejection?
6. Is dying on a given round considered an 'action', i.e. if a Hydractinia is flagged to die in a given time-step, should it be allowed to do something else before giving up the ghost?

Agent Based Simulation

In considering the first question, we decided to employ a hybrid model in which each cell of a square lattice is considered an agent in a variety of states. Empty cells are flagged as dead, and may conduct no actions. Alive cells may take one of the following actions per turn, checked in the following order:

1. Change to a dead agent with probability 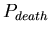$P_{death}$ at each timestep
2. In a random order, check each of the cells in the adjacent nov Neumann neighborhood for successful allorecognition. The first failure results in a fight which is immediately resolved.
3. With probability 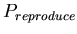$P_{reproduce}$, spawn. If reproducing, check in a random order the von Neumann neighborhood of adjacent cells for one that is empty. The first empty cell found becomes the location of the new agent.
4. If none of the above actions were taken, do nothing.

Agent Interactions

Early in our discussions, we agreed that counting the size of a particularly agent's larger community would be both problematic in terms of implementation and was only loosely representative of the real-world characteristics which this model aspect was seeking to represent. In particular, we did not see a simple way to resolve the difficulty of hostile colonies mutually recognizing a third party (i.e. the genotypes 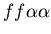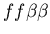$ff\alpha \alpha$, $ff\beta \beta$ and $rr\beta \beta$). 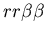Clearly in this case, the two hostile colonies should not be counted as part of the same colony, yet from the perspective of a member of the neutral colony, they should be. Fundamentally, the problem with counting colony membership arises from the fact that allorecognition is not transitive: if colony A recognizes colony B, and colony B recognizes colony C, then colony A does not necessarily recognize colony C. Because the idea of counting colony size is motivated by the sharing of resources among fused colonies, it was not clear how to resolve a situation in which colonies A shares resources with C via B, yet A and C would not normally share resources. One could potentially simply count all cells with which a cell would recognize directly or indirectly (via any number of intermediaries). However, even this approach is problematic, as one may enough up counting all cells as being part of one super colony despite may on-going internal conflicts! At some point, either arbitrary demarcations must be made, or one must accept the potential that the metric does not truly differentiate colonies in the desired way.

As such, we decided to attempt to subsume the idea that a larger colony has more resources to devote to fights into other aspects of the model and have local interactions dictate all of the model dynamics rather than a mixture of both global and local properties. As a result, we defined a set of model probability parameters which represented the rules given in the assignment description.

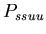• $P_{ssuu}$, the probability that a stolon-stolon or unfused-unfused fight will be won by the aggressor
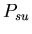• $P_{su}$, the probability that a stolon-unfused mat fight will be won by the stolon cell

Unfused mat cells obviously have an advantage over all other colonies. They can fight and, due to the increased reproductive potential that comes with nearby mat cells, reproduce faster. Setting 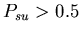$P_{su}>0.5$ gives the stolon colonies a slight advantage, which is exacerbated by having a larger colony size; however, this advantage should be mitigated by an unfused mat cell colony's greater reproductive rate. Otherwise, our model follows exactly the one described in the assignment.

We also defined the following other paramaters for our model:

• N, the length of an edge of the square lattice on which the agents may move
• t, the number of time steps over which the model runs
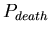• $P_{death}$, the probability at each time-step that an agent will die. The distribution of lifespans is thus a binomial one centered around $E[lifespan]= \frac{1}{P_{death}}$
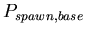• $P_{spawn, base}$, the base probability of reproducing for any morphological cell type at each time step. A binomial distribution with average $E[spawn,base]=\frac{1}{P_{spawn,base}}$
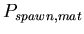• $P_{spawn, mat}$, the probability added to 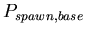$P_{spawn, base}$ for each mat cell within Manhattan distance 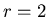$r=2$ of the spawning agent.
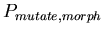• $P_{mutate, morph}$, the probability of choosing a random new morphology for the daughter cells when a cell splits
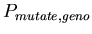• $P_{mutate, geno}$, the probability of choosing a random new chromosome (for each of the two) for the daughter cells when a cell splits

For visualization, we used the gd libraries to write color PNG image files of the cell-array at each timestep. Using the unix utility convert, we collapsed the set of image files into a MNG movie file. You can view the movies of the experiments we cite here at http://www.cs.unm.edu/brainsik/cnid/. The hues red, blue and yellow were assigned to the three morphologies, stolon, unfused mat and fused mat respectively. Combinations of saturation and value were used to differentiate the nine different genotypes possible for each of the three colors.

A link to the source code for our Hydractinia model can be found on the main Hydractinia page.